Модель сезонного авторегрессионного интегрированного скользящее среднего, SARIMA или Seasonal ARIMA, является расширением ARIMA, которая явно поддерживает одномерные данные временных рядов с сезонным компонентом.
В модель добавляет три новых гиперпараметра для указания авторегрессии (AR), разности (I) и скользящего среднего (MA) для сезонной составляющей ряда, а также дополнительный параметр для периода сезонности.
Общий вид данной модели
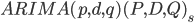
В этой модели параметры обозначают следующее:
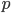— порядок модели 
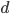— порядок интегрирования исходных данных- q — порядок модели
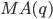
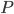— порядок сезонной составляющей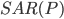 
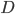— порядок интегрирования сезонной составляющей
— порядок сезонной составляющей 
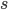— размерность сезонности(месяц, квартал и т.д.)
Используем эту модель для прогнозирования посетителей в магазине одежды. Алгоритм работы с моделью беру из книги Krispin R. Hands-On Time Series Analysis with R: Perform time series analysis and forecasting using R с некоторыми дополнениями из других источников. У нас есть данные по месячной посещаемости магазина с января 2015 по декабрь 2019.
Посмотрим на данные в датафрейме
head(df_month)
year month visit
<dbl> <dbl> <dbl>
1 2015 1 14328
2 2015 2 6974
3 2015 3 10174
4 2015 4 8994
5 2015 5 10715
6 2015 6 9381
Сделаем из датафрейма объект временного ряда и выведем его график
ts_month <- ts(data = df_month$visit,
start = c(2015, 1),
frequency = 12)
ts_plot(ts_month)
Как мы видим временной ряд имеет сезонный характер и поэтому среди семейства ARIMA моделей, модель SARIMA является наиболее подходящей моделью для использования.
Разделим ряд на обучающую и тестовую часть, для тестовой части возьмем последние 12 месяцев
ts_split <- ts_split(ts_month, sample.out = 12)
train <- ts_split$train
test <- ts_split$test
Перед тем, как начать процесс обучения модели SARIMA проведем диагностику с помощью функций ACF and PACF. Выведем их графики
ggtsdisplay(train,lag.max = 36)
Как видно, автокорреляционная функция циклична и максимумы циклов приходятся на лаги. кратные 12. Это значит, что показатель 12 шагов назад сильно влияет на текущий показатель и это логично, так как мы наблюдаем месячные данные. Это говорит о том, что например посещаемость в январе текущего года похожа на посещаемость января прошлого года и так можно сказать про любой месяц. То есть в данных мы наблюдаем ярко выраженную сезонность. Кроме того, линейное затухание сезонных лагов говорит о том, что ряд не является стационарным и требуется сезонное дифференцирование. Поэтому для моделирования ряда и дальнейшего прогнозирования выбираем модель SARIMA.
Процесс настройки параметров модели SARIMA состоит из нескольких шагов.
Одной из основных проблем прогнозирования с помощью семейства моделей ARIMA является громоздкий процесс настройки моделей. Функция auto.arima из пакета forecast предоставляет решение этой проблемы. Этот алгоритм автоматизирует процесс настройки модели ARIMA с использованием статистических данных методы идентификации как структуры ряда (стационарного или нет), так и типа (сезонного или нет). нет), и устанавливает параметры модели соответственно. Используем эту функцию для подбора модели для нашего временного ряда
ts_auto_md1 <- auto.arima(train)
ts_auto_md1
Series: train
ARIMA(0,0,0)(0,1,0)[12] with drift
Coefficients:
drift
-45.3704
s.e. 4.9285
sigma^2 estimated as 129561: log likelihood=-262.46
AIC=528.93 AICc=529.29 BIC=532.09
Как видим, функция auto.arima с настройками по умолчанию выбрала модель SARIMA(0,0,0)(0,1,0)12 с AIC=528.93, который больше чем выбранная по сетке модель.
По умолчанию auto.arima применяет более короткий поиск модели с помощью пошагового подход для сокращения времени поиска. В результате функция может пропустите некоторые модели, которые могут достичь лучших результатов. Это видно из нашего примера, модель ts_auto_md1, которую мы настроили с помощью
поиск по сетке, показала AIC 517.5 против 528.93 модели auto.arima.
Введем предварительные настройки параметров функции:
ts_auto_md2 <- auto.arima(train,
max.order = 5,
D = 1,
d = 1,
stepwise = FALSE,
approximation = FALSE)
Процесс настройки параметров модели SARIMA состоит из нескольких шагов.
- Мы устанавливаем максимальный порядок модели (то есть сумму шести параметров модели).
- Мы задаем диапазон возможных комбинаций значений параметров в соответствии с ограничение максимального порядка модели
- Мы тестируем и оцениваем каждую модель, то есть типичную методику оценки с помощью AIC или BIC
- Мы выбираем набор комбинаций параметров, которые дают наилучшие результаты
Начнем процесс настройки для нашего временного ряда, установив модельный порядок следующим образом:
p <- q <- P <- Q <- 0:2
В результате получаем 66 возможных комбинаций. Поэтому имеет смысл автоматизировать процесс поиска и создать функцию поиска по сетке для определения значений
параметров, которые минимизируют оценку AIC. Будем использовать функцию expand.grid чтобы создать датафрейм со всеми возможными комбинациями поиска
arima_grid <- expand.grid(p,q,P,Q)
names(arima_grid) <- c("p", "q", "P", "Q")
arima_grid$d <- 1
arima_grid$D <- 1
Добавим в него колонку с суммой порядков модели и ограничим эту сумму 7
arima_grid$k <- rowSums(arima_grid)
arima_grid <- arima_grid[arima_grid$k<=7,]
Теперь, когда таблица поиска сетки готова, мы можем начать процесс поиска. Мы будем использовать функция lapply для итерации по таблице поиска сетки. Эта функция будет обучать модель SARIMA и получать ее оценки AIC для каждого набора параметров в таблице поиска сетки.
arima_search <- lapply(1:nrow(arima_grid), function(i){
md <- NULL
md <- arima(train, order = c(arima_grid$p[i], 1, arima_grid$q[i]),
seasonal = list(order = c(arima_grid$P[i], 1, arima_grid$Q[i])))
results <- data.frame(p = arima_grid$p[i], d = 1, q = arima_grid$q[i],
P = arima_grid$P[i], D = 1, Q = arima_grid$Q[i],
AIC = md$aic)
}) %>% bind_rows() %>% arrange(AIC)
Посмотрим на верхние результаты таблицы поиска:
p d q P D Q AIC
1 2 1 0 0 1 0 517.4965
2 0 1 2 0 1 0 518.8617
3 1 1 1 0 1 0 518.8746
4 0 1 1 0 1 0 518.9138
5 2 1 0 0 1 1 519.2843
6 2 1 0 1 1 0 519.3153
Лучшей по оценке AIC оказалась модель SARIMA(2,1,0)(0,1,0)12
Оценим точность выбранной модели на тестовый набор. Мы будем переучивать модель, используя настройки выбранной модели:
ts_best_md <- arima(train, order = c(2,1,0),seasonal = list(order =c(0,1,0)))
Посмотрим на ее коэффициенты
ts_best_md
Call:
arima(x = train, order = c(2, 1, 0), seasonal = list(order = c(0, 1, 0)))
Coefficients:
ar1 ar2
-0.9568 -0.4876
s.e. 0.1517 0.1528
sigma^2 estimated as 126190: log likelihood = -255.75, aic = 517.5
Используем обученную модель ts_best_md для прогнозирования на тестовом наборе:
ts_test_fc <- forecast(ts_best_md, h = 12)
Оценим точность модели с помощью функции accuracy
round(accuracy(ts_test_fc, test),2)
ME RMSE MAE MPE MAPE MASE ACF1 Theil's U
Training set -50.71 303.39 205.12 -0.42 2.03 0.36 0.01 NA
Test set 177.57 301.36 263.41 2.21 3.16 0.47 -0.38 0.16
Как видим, результат получился очень неплохой, MAPE на обучающем ряде 2.03% и на тестовом 3.16%
Оценим качество прогноза на графике
test_forecast(ts_month,
forecast.obj = ts_test_fc,
test = test)
Как вы можете видеть, модель SARIMA успешно фиксирует сезонную и трендовую составляющие временного ряда.
Теперь переходим к последнему шагу - прогнозированию и формирование окончательного прогноза с помощью выбранной модели. Начнем с того, что
переучим выбранную модель по всему временному ряду :
final_md <- arima(ts_month, order = c(2,1,0), seasonal = list(order =c(0,1,0)))
Прежде чем мы спрогнозируем следующие 12 месяцев, посмотрим на остатки модели.
Ljung-Box test
data: Residuals from ARIMA(2,1,0)(0,1,0)[12]
Q* = 13.177, df = 10, p-value = 0.214
Model df: 2. Total lags used: 12
Результаты теста Юнга-бокса показали, что остатки модели являются белым шумом.
По графику остатков, вы можете увидеть, что эти остатки являются белым шумом
и нормально распределены. Кроме того, тест Юнга-бокса подтверждает отсутствие автокорреляции оставаясь на остатках с p-значением 0,214 и мы не можем отвергнуть нулевую гипотезу что остатки - это белый шум. Идем дальше, сделаем прогноз на следующие 12 месяцев работы магазина.
ts_month_fc <- forecast(final_md, h = 12)
Выведем график прогноза
Одной из основных проблем прогнозирования с помощью семейства моделей ARIMA является громоздкий процесс настройки моделей. Функция auto.arima из пакета forecast предоставляет решение этой проблемы. Этот алгоритм автоматизирует процесс настройки модели ARIMA с использованием статистических данных методы идентификации как структуры ряда (стационарного или нет), так и типа (сезонного или нет). нет), и устанавливает параметры модели соответственно. Используем эту функцию для подбора модели для нашего временного ряда
ts_auto_md1 <- auto.arima(train)
ts_auto_md1
Series: train
ARIMA(0,0,0)(0,1,0)[12] with drift
Coefficients:
drift
-45.3704
s.e. 4.9285
sigma^2 estimated as 129561: log likelihood=-262.46
AIC=528.93 AICc=529.29 BIC=532.09
Как видим, функция auto.arima с настройками по умолчанию выбрала модель SARIMA(0,0,0)(0,1,0)12 с AIC=528.93, который больше чем выбранная по сетке модель.
По умолчанию auto.arima применяет более короткий поиск модели с помощью пошагового подход для сокращения времени поиска. В результате функция может пропустите некоторые модели, которые могут достичь лучших результатов. Это видно из нашего примера, модель ts_auto_md1, которую мы настроили с помощью
поиск по сетке, показала AIC 517.5 против 528.93 модели auto.arima.
Введем предварительные настройки параметров функции:
- пошаговый аргумент stepwise, если он установлен как FALSE позволяет установить более надежный и тщательный поиск
- установим разностные параметры d и D равными 1
- ограничим порядок модели max.order = 5, он установливает порядок максимального значения суммы p+q+P+Q, учитывая d и D равными 1 максимальный порядок будет равен 7
- установим аргумент аппроксимации approximation = FALSE для более точных вычисления информационных критериев
ts_auto_md2 <- auto.arima(train,
max.order = 5,
D = 1,
d = 1,
stepwise = FALSE,
approximation = FALSE)
В результате таких настроек функция auto.arima вернет нам ту же модель, которая была сделана с помощью поиска по сетке.
ts_auto_md2
Series: train
ARIMA(2,1,0)(0,1,0)[12]
Coefficients:
ar1 ar2
-0.9568 -0.4876
s.e. 0.1517 0.1528
sigma^2 estimated as 133885: log likelihood=-255.75
AIC=517.5 AICc=518.27 BIC=522.16
Комментариев нет:
Отправить комментарий