В непрерывном распределении вероятностей переменная может принимать любое действительное число. Она не ограничена конечным набором значений, как это имеет место в дискретном распределении вероятностей, например, вес здорового новорожденного ребенка может варьироваться примерно от 2,5 до 4,5 кг
Непрерывное распределение вероятностей характеризуется функцией плотности вероятности (PDF). Сумма всех вероятностей, которые может принять случайная величина, равна 1. Таким образом, площадь под графиком функции плотности вероятности равна 1.
Так как использовать в примерах будем в основном функции библиотеки scipy.stats приведем общие принципы работы с ними :
Работа с библиотекой scipy.stats
Общий принцип:
X— некоторое распределение с параметрами params
X.rvs(size=N, params) — генерация выборки размера (Random VariateS). Возвращает
numpy.array
X.cdf(x, params) — значение функции распределения в точке (Cumulative Distribution
Function)
X.logcdf(x, params) — значение логарифма функции распределения в точке
X.ppf(q, params) — q-квантиль (Percent Point Function)
X.mean(params) — математическое ожидание
X.median(params) — медиана
X.var(params) — дисперсия (Variance)
X.std(params) — стандартное отклонение = корень из дисперсии (Standard Deviation)
Кроме того для непрерывных распределений определены функции
X.pdf(x, params) — значение плотности в точке (Probability Density Function)
X.logpdf(x, params) — значение логарифма плотности в точке
А для дискретных
X.pmf(k, params) — значение дискретной плотности в точке (Probability Mass Function)
X.logpdf(k, params) — значение логарифма дискретной плотности в точке
Параметры могут быть следующими:
loc — параметр сдвига
scale — параметр масштаба
и другие параметры (например, и для биномиального)
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Параметры в scipy.stats:
loc = $\mu$
scale =$\sigma$"
Нормальное распределение, также известное как гауссово распределение, является одним из самых популярных непрерывных распределений в области аналитики, особенно из-за его использования в нескольких контекстах. Нормальное распределение наблюдается по многим естественным показателям, таким как возраст, зарплата, объем продаж, вес при рождении, рост и т. д. Она также широко известна как кривая колокола (так как имеет форму колокола).
Нормальное распределение параметризуется двумя параметрами: средним значением распределения $\mu$ и дисперсией $\sigma^2$". Посмотрим, как изменяется форма распределения в зависимости от дисперсии :
from scipy.stats import norm
X = 2.5
dx = 0.1
R = np.arange(-X,X+dx,dx)
L = list()
sdL = (0.5,1,2,3)
for sd in sdL:
f = norm.pdf
L.append([f(x,loc=0,scale=sd) for x in R])
for sd,P in zip(sdL,L):
plt.plot(R,P,zorder=1,lw=1.5,
label="$\sigma$=" + str(sd))
plt.legend()
ax = plt.axes()
ax.set_xlim(-2.1,2.1)
ax.set_ylim(0,1.0)
plt.title("Normal distribution Pdf")
plt.ylabel("PDF at $\mu$=0, $\sigma$")
Нормальное распределение также можно рассматривать как непрерывный предел биномиального распределения $n\rightarrow \infty$. Подтверждение этому можно увидеть это на графике:
from scipy.stats import binom
cols = colors.cnames
n_values = [1, 5,10, 30, 100]
subplots = [111+100*x for x in range(0,len(n_values))]
ctr = 0
fig, ax = plt.subplots(len(subplots), figsize=(6,12))
k = np.arange(0, 200)
p=0.5
for n in n_values:
k=np.arange(0,n+1)
rv = binom(n, p)
ax[ctr].plot(k, rv.pmf(k), lw=2)
ax[ctr].set_title("$n$=" + str(n))
ctr += 1
fig.subplots_adjust(hspace=0.5)
plt.suptitle("Binomial distribution PMF (p=0.5) for various values of n", fontsize=14)
При увеличении n биномиальное распределение приближается к нормальному. На самом деле это хорошо видно на предыдущих графиках для n>=30.
Создадим случайную величину, которая следует нормальному распределению, используя scipy.stats модуль. Предположим, что рост мужчин описывается нормальным распределением со средним значением 170 см и стандартным отклонением 10 см. Чтобы создать эту случайную величину с помощью scipy. stats, нужно использовать следующий код:
heights_mean = 170
heights_sd = 10
# Создаем экземпляр объекта случайной величины
heights_rv = stats.norm(loc = heights_mean,scale = heights_sd)
Чтобы построить полную функцию плотности вероятности, мы должны создать вектор,
содержащий набор возможных значений, которые может принимать эта переменная. Предположим, что мы хотим построить функцию для значений между 130см и 210 см, которые являются вероятными значениями для здоровых взрослых мужчин. Для этого создаем вектор значений с помощью np. linspace, который в этом случае создаст 200 равноудаленных чисел между 120 и 210 (включительно):
values = np.linspace(130, 210, num=200)
Теперь можем построить график против созданных значений:heights_rv_pdf = heights_rv.pdf(values)
plt.plot(values, heights_rv_pdf)
plt.grid();
Чем выше кривая, тем более вероятны значения. Например, с большей вероятностью можно наблюдать рост мужчин между 160 и 170 см, чем между 140 и 150 см.
Теперь, когда мы определили эту нормально распределенную случайную величину, можем использовать ее для некоторых расчетов. Например можем сделать некоторую выборку из этой случайной величины. Для этого мы можем использовать метод rvs, который генерирует случайные выборки из распределения вероятностей:
sample_heighs = heights_rv.rvs\
(size = 5,random_state = 998)
for i, h in enumerate(sample_heighs):
print(f'Men {i + 1} height: {h:0.1f}')
Men 1 height: 171.2 Men 2 height: 173.3 Men 3 height: 157.1 Men 4 height: 164.9 Men 5 height: 179.1
Здесь мы имитируем выборку из пяти случайных мужчин.
Можем также использовать моделирование, чтобы ответить на вопросы о
вероятности событий, связанных с этой случайной величиной. Например, какова
вероятность найти мужчину выше 190 см? Следующий код вычисляет это
моделирование с использованием нашей ранее определенной случайной величины:
sim_size = int(1e5)
sample_heights = heights_rv.rvs\
(size = sim_size,random_state = 88)
Prob_event = (sample_heights > 190).sum()/sim_size
print(f'Probability of a male > 190 cm: {Prob_event:0.5f} \
(or {100*Prob_event:0.2f}%)')
Probability of a male > 190 cm: 0.02303 (or 2.30%)Можем сравнить полученное значение с "точным"1-heights_rv.cdf(190)Как видим, получили тоже самое значение, но в одну строку.Пример нормального распределения
Чтобы понять нормальное распределение и его применение, мы будем использовать дневную доходность акций, торгуемых на BSE (бомбейская фондовая биржа). Представьте себе сценарий, в котором инвестор хочет понять риски и доходность, связанные с различными акциями, прежде чем инвестировать в них. Для этого анализа мы оценим две акции: BEML и GLAXO. Ежедневные торговые данные (цена открытия и закрытия) по каждой акции берутся за период с 2010 по 2016 год с сайта BSE (www.bseindia.com).
Во-первых, мы загрузим и подготовим данные, прежде чем вернуться к применению нормального распределения.
beml_df = pd.read_csv('BEML.csv')
glaxo_df = pd.read_csv('GLAXO.csv')
print(beml_df.columns)
print(glaxo_df.columns)
Index(['Date', 'Open', 'High', 'Low', 'Last', 'Close', 'Total Trade Quantity',
'Turnover (Lacs)'],
dtype='object')
Index(['Date', 'Open', 'High', 'Low', 'Last', 'Close', 'Total Trade Quantity',
'Turnover (Lacs)'],
dtype='object')Набор данных содержит дневную цену открытия (Open) и закрытия (Close) , а также дневные максимумы (High) и минимумы цен (Low) , общий объем торговли (Total Trade Quantity) ,количество и оборот (Turnover (Lacs)). Будем рассматривать только цены закрытия. Дневная доходность акции рассчитывается как изменение цены закрытия по отношению к цене закрытия вчерашнего дня.
Поскольку наш анализ будет включать только дневные цены закрытия, поэтому мы выберем столбцы даты и закрытия из фреймов данных.
beml_df = beml_df[['Date', 'Close']]
glaxo_df = glaxo_df[['Date', 'Close']]
Визуализация дневных цен закрытия покажет, как цены акций двигались с течением времени. Чтобы показать тренд цены закрытия, строки должны быть упорядочены по времени. Фреймы данных имеют столбец date, поэтому мы можем создать индекс DatetimeIndex из этого столбца Date. Это гарантирует, что строки будут отсортированы по времени в порядке возрастания.
glaxo_df = glaxo_df.set_index(pd.DatetimeIndex(glaxo_df['Date']))
beml_df = beml_df.set_index(pd.DatetimeIndex(beml_df['Date']))
Покажем первые 5 записей после того, как фрейм данных будет отсортирован по времени, чтобы убедимся, что это сделано правильно
| Date | Date Close | |
|---|---|---|
| Date | ||
| 2010-01-04 | 2010-01-04 | 1625.65 |
| 2010-01-05 | 2010-01-05 | 1616.80 |
| 2010-01-06 | 2010-01-06 | 1638.50 |
| 2010-01-07 | 2010-01-07 | 1648.70 |
| 2010-01-08 | 2010-01-08 | 1639.80 |
Теперь построим график тренда цен закрытия акций GLAXO
import matplotlib.pyplot as plt
import seaborn as sn
%matplotlib inline
plt.plot(glaxo_df.Close)
plt.xlabel('Time')
plt.ylabel('Close Price')
plt.title('glaxo stock')
Теперь построим график ценового тренда закрытия акций BEML.
plt.plot(beml_df.Close)
plt.xlabel('Time')
plt.ylabel('Close Price')
plt.title('beml stock')
Можно заметить, что в период 2010-2017 годов наблюдается тенденция к росту цены закрытия Glaxo. Однако BEML имел тенденцию к снижению в течение 2010-2013 годов, за которой последовала тенденция к росту с 2014 года, а затем снова коррекция цен с середины 2015 года.
Инвестор заинтересован в понимании следующих характеристик этих акций:
1. Какова ожидаемая доходность этих акций?
2. Какие акции имеют более высокий риск или волатильность с точки зрения ежедневной доходности?
3. Каков ожидаемый диапазон доходности для 95% доверительного интервала?
4. какая акция имеет более высокую вероятность получения ежедневной прибыли в размере 2% или более?
5. Какая акция имеет более высокую вероятность получения убытка (риска) в размере 2% или более?
Чтобы ответить на вышеприведенные вопросы, мы должны выяснить поведение ежедневной доходности (мы будем называть это прибылью ) на этих акциях. Прибыль может быть рассчитана как процентное изменение цены закрытия от цены закрытия предыдущего дня.
$$gain=\frac{ClosePrice_{t}-ClosePrice_{t-1}}{ClosePrice_{t-1}}$$
Метод pct_change () в Pandas даст процентное изменение значения столбца, сдвинутого на период, который передается в качестве параметра периодам periods = 1 указывает на изменение значения с момента последней строки, то есть за предыдущий день.
glaxo_df['gain'] = glaxo_df.Close.pct_change(periods = 1)
beml_df['gain'] = beml_df.Close.pct_change(periods = 1)
glaxo_df.head(5)
| Date | Close | gain | |
|---|---|---|---|
| Date | |||
| 2010-01-04 | 2010-01-04 | 1625.65 | NaN |
| 2010-01-05 | 2010-01-05 | 1616.80 | -0.005444 |
| 2010-01-06 | 2010-01-06 | 1638.50 | 0.013422 |
| 2010-01-07 | 2010-01-07 | 1648.70 | 0.006225 |
| 2010-01-08 | 2010-01-08 | 1639.80 | -0.005398 |
Выигрыш первого дня отображается как NAN, так как нет предыдущего дня для расчета выигрыша. Мы можем отбросить эту
запись с помощью метода dropna ().
glaxo_df = glaxo_df.dropna()
beml_df = beml_df.dropna()
Построим временной график изменения прибыли
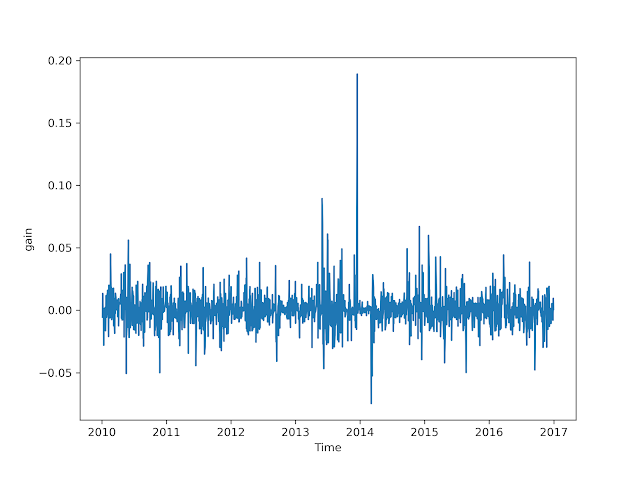
plt.figure(figsize = (8, 6))
plt.plot(glaxo_df.index, glaxo_df.gain)
plt.xlabel('Time')
plt.ylabel('gain')
График показывает, что дневной прирост является весьма случайным и колеблется около 0.00. Прирост остается в основном между 0,05 и -0,05. Однако один раз наблюдался очень высокий выигрыш, близкий к 0,20 , и точно так же один раз наблюдалась высокая потеря около 0,08. Чтобы получить лучшее представление выведем гистограмму с наложением функции плотности :
sn.distplot(glaxo_df.gain, label = 'Glaxo')
sn.distplot(beml_df.gain, label = 'BEML')
plt.xlabel('gain')
plt.ylabel('Density')
plt.legend()
Судя по графику, прибыль, по-видимому, нормально распределена для обеих акций со средним значением около 0,00. Beml, по-видимому, имеет более высокую дисперсию, чем Glaxo.
Нормальное распределение параметризуется двумя параметрами: средним значением распределения $\mu$ и дисперсией $\sigma^2$".
Методы mean() и std () для столбцов фрейма данных возвращают среднее значение и стандартное отклонение соответственно.
Среднее и стандартное отклонение дневной доходности для Glaxo составляют:
print('Daily gain of Glaxo')
print('---------------------')
print('Mean: ', round(glaxo_df.gain.mean(), 4))
print('Standard Deviation: ', round(glaxo_df.gain.std(), 4))
Daily gain of Glaxo --------------------- Mean: 0.0004 Standard Deviation: 0.0134
Среднее и стандартное отклонение дневной доходности для BEML составляют:
print('Daily gain of BEML')
print('---------------------')
print('Mean: ', round(beml_df.gain.mean(), 4))
print('Standard Deviation: ', round(beml_df.gain.std(), 4))
Daily gain of BEML --------------------- Mean: 0.0003 Standard Deviation: 0.0264Метод describe выводит подробную таблицу основных статистикbeml_df.gain.describe()Ожидаемая дневная норма доходности (прибыли) составляет около 0% для обеих акций. Дисперсия или стандартное отклонение прибыли указывает на риск. Таким образом, акции BEML имеют более высокий риск, так как стандартное отклонение BEML составляет 2,64% тогда как стандартное отклонение для Glaxo составляет 1,33%. Доверительный ИнтервалЧтобы выяснить, каков ожидаемый диапазон доходности для 95% доверительного интервала, нам нужно вычислить значения прибыли для двух стандартных отклонений от среднего по обе стороны распределения, то есть m ± 2s .Для этого используем метод stats.norm.interval, он принимает три параметра :1. alpha: это интервал, например, 0,9 для 90% доверительного интервала. 2. loc: это параметр местоположения для распространения. Это среднее значение для нормального распределения. 3. scale: это параметр масштаба распределения. Это стандартное отклонение для нормального распределения.glaxo_df_ci = stats.norm.interval( 0.95, loc = glaxo_df.gain.mean(), scale = glaxo_df.gain.std()) print( 'Gain at 95% confidence interval is: ', np.round(glaxo_df_ci, 4))Результат, возвращаемый методом, представляет собой кортеж. Первое значение кортежа - это крайнее левое значение интервала , а второе - самое правое значение интервала. Для 95% доверительного интервала прирост Glaxo остается между -2,58% и 2,66%.Доходность для BEML для 95% доверительного интервала определяетсяbeml_df_ci = stats. norm.interval(0.95, loc=beml_df.gain.mean(), scale=beml_df.gain.std()) print('Gain at 95% confidence interval is:', np.round(beml_df_ci, 4))Следовательно, прирост BEML остается между -5,15% и 5,21% для 95% доверительного интервала.Кумулятивное распределение вероятностейЧтобы вычислить вероятность выигрыша выше 2% и более, нам нужно выяснить, какова сумма всех вероятностей, что выигрыш может принимать значения больше 0,02 (то есть 2%). Функция плотности вероятности f (xi) определяется как вероятность того, что значение случайной величины X лежит между бесконечно малым интервалом, определяемым xi и xi + δx. Кумулятивная функция распределения F (a) - это область под функцией плотности вероятности до X = a. КумулятивнаяЧтобы вычислить вероятность того, что прибыль акций будет меньше -0,02 (то есть убыток), кумулятивная функция распределения может быть использована для вычисления площади распределения от крайней левой точки до -0,02.Функция stats.norm.cdf() возвращает интегральная функция распределения для нормального распределения.print('Probability of making 2% loss or higher in Glaxo: ') stats.norm.cdf( -0.02,loc=glaxo_df.gain.mean(),scale=glaxo_df.gain.std())print('Probability of making 2% loss or higher in BEML:') stats.norm.cdf( -0.02, loc=beml_df.gain.mean(), scale=beml_df.gain.std())Значение кумулятивной функции распределения указывает на то, что Beml имеет вероятность 22,1%, в то время как Glaxo имеет только 6,35% вероятности потери 2% или выше. Аналогично, вероятность получения ежедневного выигрыша в 2% или выше будет задана областью справа от 0,02 распределения. Поскольку stats.norm.cdf() дает кумулятивную площадь слева, вероятность может быть вычислена путем вычитания значения кумулятивной функции распределения из 1.print('Probability of making 2% gain or higher in Glaxo:', 1 - stats.norm.cdf(0.02, loc=glaxo_df.gain.mean(), scale=glaxo_df.gain.std())) print('Probability of making 2% gain or higher in BEML:', 1 - stats.norm.cdf(0.02, loc=beml_df.gain.mean(), scale=beml_df.gain.std()))Вероятность получения выигрыша в 2% и более для Glaxo составляет 7,1%, тогда как для BEML-22,76%.
Непрерывное равномерное распределение
Равномерное распределение моделирует случайную величину X, которая может принимать любое значение в диапазоне [a, b] с равной вероятностью.
Функция плотности вероятности для равномерного распределения имеет вид
Для a <= x <= b
$$f(x)=\frac{1}{b-a}$$
и 0 для остальных значений
Математическое ожидание и дисперсия задаются соответственно следующими выражениями:
$$E(x)=\frac{a+b}{2}$$
$$Var(x)=\frac{b-a}{12}$$
Параметры в scipy.stats:
loc = a
scale = b-a
Непрерывное равномерное распределение вероятностей генерируется и строится для различных размеров выборки в следующем коде:
np.random.seed(100)
ctr = 0
fig, ax = plt.subplots(3, figsize=(10,12))
nsteps=10
for i in range(0,3):
cud = np.random.uniform(0,1,nsteps) # generate distrib
count, bins, ignored = ax[ctr].hist(cud,15,density=True)
ax[ctr].plot(bins,np.ones_like(bins),linewidth=2, color='r')
ax[ctr].set_title('sample size=%s' % nsteps)
ctr += 1
nsteps *= 100
fig.subplots_adjust(hspace=0.4)
plt.suptitle("Continuous Uniform probability distributions for \
various sample sizes" , fontsize=14)







Комментариев нет:
Отправить комментарий