Машинное обучение с Python в розничной торговле : метрики качества в задачах регрессии

Рассмотрим часто используемые метрики качества модели : MAE,MPE,MAPE,MSE,RMSE,R2 в задачах регрессии

Введем следующие обозначения:
$y$ - представляет фактическое значение в момент времени t.
$\hat{y}$ - представляет собой прогнозируемое значение

$\bar{y}$ - среднее значение
$e=y-\hat{y}$ - представляет собой ошибку прогноза (остаточную) 
n - количество наблюдений

Средняя абсолютная ошибка прогноза ( mean absolute error - MAE)

$$MAE=\frac{1}{n}\sum_{1}^{n}\left | e \right |$$
среднее значение всех ошибок прогноза по абсолютной величине, показывает на величину общей погрешности
Желательны небольшие значения MAE.
Зависит от масштаба измерений и преобразования данных.

Не наказывает экстремальные значения ошибок.

Средняя процентная ошибка (mean percentage error  - MPE)

$$MPE=\frac{1}{n} \sum_{1}^{n}\left ( \frac{e}{y} \right )*100$$
средний процент ошибок, величина и знак показывает смещение прогноза относительно фактических значений в процентах

Желательно, чтобы MPE был близок к нулю.

Средняя абсолютная процентная ошибка (mean absolute percentage error - MAPE)

$$MAPE=\frac{1}{n} \sum_{1}^{n}\left | \frac{e}{y} \right |*100$$
средняя абсолютная ошибка в процентах без знака ошибки.
Зависит от преобразование данных, но не от масштаба измерений

Не наказывает экстремальные значения ошибок.

Среднеквадратичная ошибка (mean squared error - MSE)

$$MSE=\frac{1}{n}\sum_{1}^{n}e^{2}$$
средняя квадратичная ошибка, подчеркивает большие ошибки за счет возведения каждой ошибки в квадрат.

Корень среднеквадратичной ошибки (root mean squared error - RMSE)

$$RMSE=\sqrt{MSE}=\sqrt{\frac{1}{n}\sum_{1}^{n}e^{2}}$$

Такие же свойства как MSE

R-squared

Еще одна полезная метрика,  называется коэффициентом детерминации, или статистикой R-квадрат. $R^{2}$-варьирует в интервале от 0 до 1 и измеряет долю вариации в данных, объясняемую в модели. Он полезен главным образом в объяснительных применениях регрессии, где надо определить, насколько хорошо модель подогнана к данным. Формула для $R^{2}$ :

$$R^{2}=1-\frac{\sum \left ( y-\hat{y} \right )^2}{\sum \left ( y-\bar{y} \right )^2}$$

Какую метрику использовать

𝑅2 значение очень интуитивно понятно. Но исследования показывают, что 𝑅2 действителен только для линейной регрессии. Однако большинство моделей регрессии, такие например  как дерево решений или KNN, являются нелинейными моделями. Для нелинейных моделей мы не можем полностью доверять 𝑅2. Предпочтительно всегда использовать 𝑅2 вместе с другими показателями, такими как MAE и RMSE. Когда необходимо  уменьшить влияние выбросов, лучше  использовать MAE, когда выбросы нельзя игнорировать, лучше использовать RMSE.

Для окончательного представления результатов, после того, как модель выбрана, с моей точки зрения лучше всего подходят 𝑅2 и MAPE, которые показывают насколько модель улавливает изменение объясняемой переменной и процентное отклонение ошибки.

Для примера расчета представленных метрик качества рассмотрим задачу регрессии выручки розничных магазинов одежды. 

Загружаем данные из файла Excel и выводим первые и последние пять строк

df = pd.read_excel("shops83.xlsx")

pd.concat([df.head(), df.tail()])

shop	rev	visit	balance	dress_room	store_age	type
0	sh1	6.598924e+06	4785	1.927292e+07	8	14	1
1	sh2	3.747408e+06	4563	1.636130e+07	8	14	1
2	sh3	3.174413e+06	4502	1.041671e+07	8	14	1
3	sh4	4.273869e+06	4476	1.679955e+07	8	14	1
4	sh5	3.158587e+06	4261	1.537624e+07	8	14	1
78	sh79	1.499151e+06	1234	9.071280e+06	4	5	3
79	sh80	2.118645e+06	1839	1.236749e+07	6	4	3
80	sh81	1.849056e+06	1655	1.107211e+07	4	4	2
81	sh82	2.218297e+06	1636	1.284459e+07	4	4	2
82	sh83	2.258007e+06	2123	1.250146e+07	6	3	2

Где :

• shop - индекс магазина
• rev - месячная выручка в рублях
• visit - количество посетителей
• balance - средний товарный остаток в рублях
• dress_room - количество примерочных
• store_age - количество полных отработанных магазином лет
• type - тип магазина : 1 - крупный торговый центр, 2 - районный торговый центр, 
• 3 -магазин у дома

#Сделаем новый датафрейм без индекса магазина, он нам для расчета не нужен

df1 = df.iloc[:,1:7]

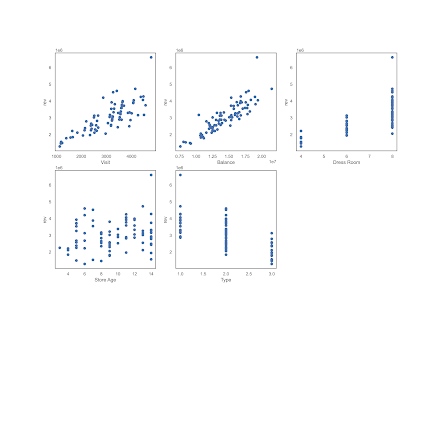
Оценим визуально связь между выручкой и остальными переменными :

plt.figure(figsize=(15,10.5))

plt.figure(figsize=(15,15))

plot_count = 1

for feature in list(df1.columns)[1:]:

    plt.subplot(3,3,plot_count)

    plt.scatter(df1[feature], df1['rev'])

    plt.xlabel(feature.replace('_',' ').title())

    plt.ylabel('rev')

    plot_count+=1

Визуально можно уверенно утверждать о наличии связи выручки с посетителями, товарным остатком, количеством примерочных и типом магазина, связь с "возрастом" магазина расплывчато слабая.

Выведем корреляционную матрицу

df1corr = df1.corr(method="pearson")

sns.heatmap(df1corr, annot=True,annot_kws={"size":12},cmap="coolwarm")

Как видим, она подтверждает предположения, сделанные на основе визуализации.

Преобразуем "Тип" в дамми-переменную и перейдем непосредственно к регрессии и оценке ее качества

df1['type_'] = df1.type

df1 = pd.get_dummies(df1, columns=["type_"], prefix=["type"],drop_first=True)

df1

rev	visit	balance	dress_room	store_age	type	type_2	type_3
0	6.598924e+06	4785	1.927292e+07	8	14	1	0	0
1	3.747408e+06	4563	1.636130e+07	8	14	1	0	0
2	3.174413e+06	4502	1.041671e+07	8	14	1	0	0
3	4.273869e+06	4476	1.679955e+07	8	14	1	0	0
4	3.158587e+06	4261	1.537624e+07	8	14	1	0	0
...	...	...	...	...	...	...	...	...
78	1.499151e+06	1234	9.071280e+06	4	5	3	0	1
79	2.118645e+06	1839	1.236749e+07	6	4	3	0	1
80	1.849056e+06	1655	1.107211e+07	4	4	2	1	0
81	2.218297e+06	1636	1.284459e+07	4	4	2	1	0
82	2.258007e+06	2123	1.250146e+07	6	3	2	1	0

Выделим зависимую и объясняющие переменные (предикторы) и разделим их на обучающую и тестовую части.

y_col = "rev"

x = df1.drop(y_col, axis=1)

y = df1[y_col]

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=23)

Также определим две вспомогательные функции : для расчета MAPE и для визуализации остатков модели по обучающей и тестовой части :

Функция для расчета MAPE

def MAPE(Y_actual,Y_Predicted):

    mape = np.mean(np.abs((Y_actual - Y_Predicted)/Y_actual))*100

    return mape

Функция для визуализации остатков модели

def plot_residual_vs_predicted(y_train, y_test,y_train_pred, y_test_pred, y_name, model_name):

    x_max = np.max([np.max(y_train_pred), np.max(y_test_pred)])

    x_min = np.min([np.min(y_train_pred), np.min(y_test_pred)])

    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6), sharey=True)

    ax1.scatter(y_train_pred, y_train_pred - y_train,c='steelblue',

                marker='o', edgecolor='white',label='Training data')

    ax2.scatter(y_test_pred, y_test_pred - y_test,c='limegreen',

                marker='s',edgecolor='white',label='Test data')

    ax1.set_ylabel('Residuals')

    for ax in (ax1, ax2):

        ax.set_xlabel('Predicted values')

        ax.set_xlabel(f"Predicted values : {y_name}", fontsize=12)

        ax.legend(loc='upper left')

        ax.hlines(y=0, xmin=x_min*0.8, xmax=x_max*1.2,\

        color='black', lw=2)

        ax.set_title(f"Residual vs. Predicted: {model_name}", fontsize=18)

    plt.tight_layout()

    plt.show()

Рассмотрим три модели регрессии из библиотеки scikit-learn : линейная регрессия, решающие деревья и модель случайного леса.

Модель линейной регрессии

from sklearn.linear_model import LinearRegression

# Создаем модель

reg = LinearRegression()

# Обучаем

reg.fit(x_train, y_train)

# Рассчитываем прогноз на тестовых данных

pred = reg.predict(x_test)

# Рассчитываем метрики качества

mae = metrics.mean_absolute_error(y_test, pred)

mse = metrics.mean_squared_error(y_test, pred)

mape = MAPE(y_test, pred)

rmse = math.sqrt(mse)

r2 = metrics.r2_score(y_test, pred)

# Выводим метрики

print('Decision Linear Regression Metrics:')

print(f'R^2 Score                  = {r2:.3f}')

print(f'Mean Absolute Percentage Error    = {mape:.2f}')

print(f'Mean Absolute Error        = {mae:.2f}')

print(f'Mean Squared Error         = {mse:.2f}')

print(f'Root Mean Squared Error    = {rmse:.2f}')

Decision Linear Regression Metrics:
R^2 Score                  = 0.898
Mean Absolute Percentage Error    = 7.43
Mean Absolute Error        = 221822.81
Mean Squared Error         = 67624241979.47
Root Mean Squared Error    = 260046.62

Модель решающих деревьев

from sklearn.tree import DecisionTreeRegressor

dtr = DecisionTreeRegressor(random_state=23)

dtr.fit(x_train, y_train)

pred = dtr.predict(x_test)

mae = metrics.mean_absolute_error(y_test, pred)

mse = metrics.mean_squared_error(y_test, pred)

mape = MAPE(y_test, pred)

rmse = math.sqrt(mse)

r2 = metrics.r2_score(y_test, pred)

print('Decision Tree Regression Metrics:')

print(f'R^2 Score                  = {r2:.3f}')

print(f'Mean Absolute Percentage Error    = {mape:.2f}')

print(f'Mean Absolute Error        = {mae:.2f}')

print(f'Mean Squared Error         = {mse:.2f}')

print(f'Root Mean Squared Error    = {rmse:.2f}')

Decision Tree Regression Metrics:
R^2 Score                  = 0.686
Mean Absolute Percentage Error    = 12.01
Mean Absolute Error        = 375147.27
Mean Squared Error         = 207404257548.56
Root Mean Squared Error    = 455416.58

Модель случайного леса

from sklearn.ensemble import RandomForestRegressor

rfr = RandomForestRegressor(n_estimators=10, random_state=23)
rfr.fit(x_train, y_train)
pred = rfr.predict(x_test)


mae = metrics.mean_absolute_error(y_test, pred)
mse = metrics.mean_squared_error(y_test, pred)
mape = MAPE(y_test, pred)
rmse = math.sqrt(mse)
r2 = metrics.r2_score(y_test, pred)

# Display metrics
print('Decision Tree Regression Metrics:')
print(f'R^2 Score                  = {r2:.3f}')
print(f'Mean Absolute Percentage Error    = {mape:.2f}')
print(f'Mean Absolute Error        = {mae:.2f}')
print(f'Mean Squared Error         = {mse:.2f}')
print(f'Root Mean Squared Error    = {rmse:.2f}')

Decision Tree Regression Metrics:
R^2 Score                  = 0.811
Mean Absolute Percentage Error    = 9.55
Mean Absolute Error        = 286793.10
Mean Squared Error         = 124795457672.01
Root Mean Squared Error    = 353264.01

Далее мы должны посмотреть как связаны остатки с предсказанными значениями

Остатки модели линейной регрессии

y_train_pred = reg.predict(x_train)
y_test_pred = reg.predict(x_test)
plot_residual_vs_predicted(y_train, y_test,y_train_pred, y_test_pred, 

'rev', 'LinearRegression')

Остатки модели решающих деревьев

y_train_pred = dtr.predict(x_train)
y_test_pred = dtr.predict(x_test)
plot_residual_vs_predicted(y_train, y_test,y_train_pred, y_test_pred, 

'rev', 'Decision Tree')

Остатки модели случайного леса

y_train_pred = reg.predict(x_train) y_test_pred = reg.predict(x_test) plot_residual_vs_predicted(y_train, y_test,y_train_pred, y_test_pred, 'rev', 'Random Forest')

Видим, что у моделей линейной регрессии и случайного леса остатки боле менее равномерно разбросаны относительно нуля. На тестовой выборке характер разброса у этих моделей очень похож, это было видно и по близким значениям метрик качества. График остатков модели решающих деревьев показывает переобучение на обучающей выборке и больший разброс на тестовой.

Как видим, лучший результат по метрикам качества показала модель линейной регрессии. На ней и остановимся. Для этой модели в части продолжения ее анализа, надо посмотреть как связаны остатки с предикторами, которые включены в модель. У нас имеется два непрерывных предиктора  и три дискретных, определим новую функцию для построения графиков остатков и посмотрим на них.

def plot_residual_vs_feature(x_train,x_test,y_train, y_test,y_train_pred, y_test_pred, feature_name, model_name):

    x_max = np.max([np.max(x_train), np.max(x_test)])

    x_min = np.min([np.min(x_train), np.min(y_test)])

    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6), sharey=True)

    ax1.scatter(x_train, y_train_pred - y_train,c='steelblue',

                marker='o', edgecolor='white',label='Training data')

    ax2.scatter(x_test, y_test_pred - y_test,c='limegreen',

                marker='s',edgecolor='white',label='Test data')

    ax1.set_ylabel('Residuals')

    for ax in (ax1, ax2):

        ax.set_xlabel('Feature values')

        ax.set_xlabel(f"Feature values : {feature_name}", fontsize=12)

        ax.legend(loc='upper left')

        ax.hlines(y=0, xmin=x_min*0.8, xmax=x_max*1.2,\

        color='black', lw=2)

        ax.set_title(f"Residual vs. Feature: {model_name}", fontsize=18)

    plt.tight_layout()

    plt.show()

Модель линейной регрессии предиктор : посетители

predicted = reg.predict(x_test)

plot_residual_vs_feature(x_train['visit'],x_test['visit'],y_train, y_test,y_train_pred,

                         y_test_pred, 'visit', 'LinearRegression')

Остатки распределено приблизительно равномерно, особых проблем нет.

Модель линейной регрессии предиктор : средний остаток товара в розничных ценах

plot_residual_vs_feature(x_train['balance'],x_test['balance'],y_train, y_test,y_train_pred,y_test_pred, 'balance', 'LinearRegression')

Остатки распределено приблизительно равномерно, особых проблем нет.

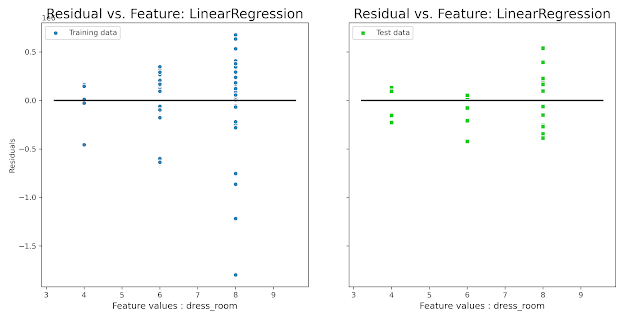
Модель линейной регрессии предиктор : количество примерочных

plot_residual_vs_feature(x_train['dress_room'],x_test['dress_room'],y_train, y_test,y_train_pred,y_test_pred, 'dress_room', 'LinearRegression')

Разброс на обучающей части симметричен относительно нуля, на тестовой в силу меньшего количества значений есть небольшое смещение в сторону занижения, но в принципе результат нормальный.

Модель линейной регрессии предиктор : "возраст магазина"

plot_residual_vs_feature(x_train['store_age'],x_test['store_age'],y_train, y_test,y_train_pred,y_test_pred, 'store_age', 'LinearRegression')

Остатки распределено приблизительно равномерно, особых проблем нет.

Модель линейной регрессии предиктор : тип магазина

plot_residual_vs_feature(x_train['type'],x_test['type'],y_train, y_test,y_train_pred,

                         y_test_pred, 'type', 'LinearRegression')

На обучающей распределение близко к симметричному, на тестовой у типа 1 смещение к завышению, а у типа 3 к занижению, при дальней шей работе с моделью следует это учесть.

Итак, на примере данных по выручке 83 розничных магазинов одежды была рассмотрена задача регрессии выручки по шести показателям. Рассмотрены три вида модели и на основании метрик качества выбрана лучшая модель. Также визуально проанализированы остатки моделей.